I've been long puzzled by the fact that our brains can easily switch between working with classes and individual instances that represent those classes. Leveraging the idea that polychronous groups may represent symbols in the brain we can try to answer questions related to representation of classes and instances:
- Are there symbols that represent classes, instances, or both?
- Can a single symbol represent both, depending on how it's activated?
- How do we define/measure "closiness" of two symbols? For example, is the sun closer to a tree than a submarine? Do we measure "closiness" in terms of activity/effort to undertake to go from one symbol to another one?

Jeffrey Elman in his papers Finding Structure in Time and An Alternative View of the Mental Lexicon provides answers to these questions by using a model based on a simple recurrent network (SRN) where hidden unit patterns are fed back to themselves serving as the context for subsequent input patterns. The network was trained to predict the next word based on a corpus of sentences that were generated by a simple artificial grammar. The network was presented with words one by one and was tasked with predicting the next word. The network learned to predict words that were grammatically possible depending on the context.
Elman then looked at how the network categorized captured information. To analyze the similarity structure he averaged hidden unit activations for each word+context combination (after completing the learning phase) and then calculated Euclidian distance between generated vectors for each word. The network learned to partition network's "mental" space into major categories, which were further subdivided into smaller categories (like humans or food).
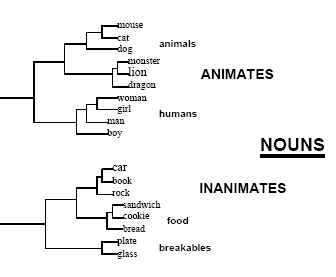
There are several interesting things about this category structure.
- It appears to be hierarchical.
- This structure is "soft" and implicit, with some categories being quite distinct and others having less distinct boundaries and sharing properties with other categoires.
- The content of the categories and their structure is not known to the network.
- Network's representations are highly context-dependent, which means that there could be separate representations for the same word that occurs in every different context. All concepts are expressed in a distributed manner as activation patters over a fixed number of nodes. A given node participates in representing multiple concepts. The activation of an individual node may be uninterpretable in isolation -- it is the activation pattern that is meaningful in its entirety. (Finding Structure in Time; p.21)
One can clearly see some parallels between this description and ideas expressed in the previous post on symbols and polychronous groups.
Capturing information about instances rather than classes provides even more benefits because "this notion of categories as emergent from the location in a high-dimensional state space, in which at any given moment different dimensions might be attended to and others ignored, suggests that different viewing perspectives on that space might yield new categories." (An Alternative View of the Mental Lexicon; p.4) Also, once in place, this category structure supports generalization as every new word, identified as belonging to an existing category, inherits all the properties that are assigned to that category. Compare this with the prototype principle expressed in Godel, Escher, Bach (p.352) as:
The most specific event can serve as a general example of a class of events.
You may notice that all those categories that "emerge" as the result of this hierarchical clustering are not explicitly represented in the model; an external observer attaches a label of "animates" or "inanimates" to groups of instances that represent those classes. How would a label like this, for example, "animates" be represented? I think it would not necessarily belong to the same space that is occupied by the instances in the class it represents; rather its relationships with items in that class or category would be rule-based ("I know if something moves on it's own, it's part of the animates class").
Elman's paper doesn't specifically address the related case of category splitting: how do we acquire "labrador" or "cocker spaniel" category after acquiring the "dog" category? From that we can go to "Snoopy", which may be an instance of the "cocker spaniel" category, or even to "my dog Snoopy".
Overall, it seems like even a simple recurring network can produce quite complex results. It might be interesting to replace hidden and context units with polychronous groups and see whether it's possible to reproduce Elman's results. I see at least two challenges with using the group approach: one is proper assignment of input and output units (how do you read the state "group A is active") and the second is measurement of "closeness" of two groups to do clustering analysis.
Leave a comment